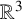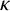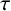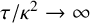2 results
CURVATURE-TORSION ENTROPY FOR TWISTED CURVES UNDER CURVE SHORTENING FLOW
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 11 July 2023, pp. 571-580
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-collapsing in homogeneity greater than one via a two-point method for a special case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 24 January 2019, pp. 1627-1635
- Print publication:
- December 2019
-
- Article
- Export citation