1 results
Scaling limits for a random boxes model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 51 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 03 September 2019, pp. 773-801
- Print publication:
- September 2019
-
- Article
- Export citation
-
We consider random rectangles in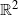
$\mathbb{R}^2$
that are distributed according to a Poisson random measure, i.e. independently and uniformly scattered in the plane. The distributions of the length and the width of the rectangles are heavy tailed with different parameters. We investigate the scaling behaviour of the related random fields as the intensity of the random measure grows to infinity while the mean edge lengths tend to zero. We characterise the arising scaling regimes, identify the limiting random fields, and give statistical properties of these limits.
