1 results
Optimal natural dualities: the role of endomorphisms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 269-296
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation

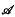 , generated by a finite algebra
, generated by a finite algebra 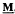 , has been introduced by Davey and Priestley in the 1990s. Since every optimal duality is determined by a transversal of a certain family of subsets of Ω, where Ω is a given set of relations yielding a duality on
, has been introduced by Davey and Priestley in the 1990s. Since every optimal duality is determined by a transversal of a certain family of subsets of Ω, where Ω is a given set of relations yielding a duality on 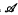 , an understanding of the structures of these subsets—known as globally minimal failsets—was required. A complete description of globally minimal failsets which do not contain partial endomorphisms has recently been given by the author and H. A. Priestley. Here we are concerned with globally minimal failsets containing endomorphisms. We aim to explain what seems to be a pattern in the way endomorphisms belong to these failsets. This paper also gives a complete description of globally minimal failsets whose minimal elements are automorphisms, when
, an understanding of the structures of these subsets—known as globally minimal failsets—was required. A complete description of globally minimal failsets which do not contain partial endomorphisms has recently been given by the author and H. A. Priestley. Here we are concerned with globally minimal failsets containing endomorphisms. We aim to explain what seems to be a pattern in the way endomorphisms belong to these failsets. This paper also gives a complete description of globally minimal failsets whose minimal elements are automorphisms, when 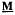 is a subdirectly irreducible lattice-structured algebra.
is a subdirectly irreducible lattice-structured algebra.