We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper we study the abstract convex program
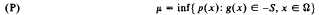
where S is an arbitrary convex cone in a finite dimensional space, Ω is a convex set and p and g are respectively convex and S (on Ω). We use the concept of a minimal cone for (P) to correct and strengthen a previous characterization of optimality for (P), see Theorem 3.2. The results presented here are used in a sequel to provide a Lagrange multiplier theorem for (P) which holds without any constraint qualification.
