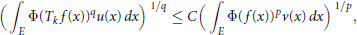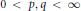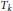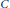We establish sufficient conditions on the weight functions  $u$ and
$u$ and  $v$ for the validity of the multidimensional weighted inequality
$v$ for the validity of the multidimensional weighted inequality
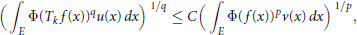 $${{\left( \int_{E}{\Phi {{\left( {{T}_{k}}f\left( x \right) \right)}^{q}}u\left( x \right)dx} \right)}^{1/q}}\,\le \,C{{\left( \int_{E}{\Phi {{\left( f\left( x \right) \right)}^{p}}v\left( x \right)dx} \right)}^{1/p}},$$
$${{\left( \int_{E}{\Phi {{\left( {{T}_{k}}f\left( x \right) \right)}^{q}}u\left( x \right)dx} \right)}^{1/q}}\,\le \,C{{\left( \int_{E}{\Phi {{\left( f\left( x \right) \right)}^{p}}v\left( x \right)dx} \right)}^{1/p}},$$
where 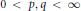 $0\,<\,p,\,q\,<\,\infty $,
$0\,<\,p,\,q\,<\,\infty $, 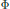 $\Phi $ is a logarithmically convex function, and
$\Phi $ is a logarithmically convex function, and 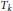 ${{T}_{k}}$ is an integral operator over star-shaped regions. The condition is also necessary for the exponential integral inequality. Moreover, the estimation of
${{T}_{k}}$ is an integral operator over star-shaped regions. The condition is also necessary for the exponential integral inequality. Moreover, the estimation of 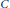 $C$ is given and we apply the obtained results to generalize some multidimensional Levin–Cochran-Lee type inequalities.
$C$ is given and we apply the obtained results to generalize some multidimensional Levin–Cochran-Lee type inequalities.