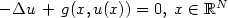We study the existence of spatial periodic solutions for nonlinearelliptic equations $- \Delta u \, + \, g(x,u(x)) = 0, \;x \in {\mathbb R}^N$ 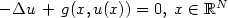 where g is a continuous function, nondecreasing w.r.t. u. Wegive necessary and sufficient conditions for the existence ofperiodic solutions. Some cases with nonincreasing functions gare investigated as well. As an application we analyze themathematical model of electron beam focusing system and we provethe existence of positive periodic solutions for the envelopeequation. We present also numerical simulations.
where g is a continuous function, nondecreasing w.r.t. u. Wegive necessary and sufficient conditions for the existence ofperiodic solutions. Some cases with nonincreasing functions gare investigated as well. As an application we analyze themathematical model of electron beam focusing system and we provethe existence of positive periodic solutions for the envelopeequation. We present also numerical simulations.