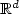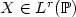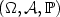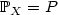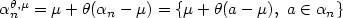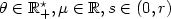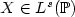We investigate in this paper the properties of some dilatations or contractions of a sequence (αn)n≥1 of Lr -optimal quantizers of an $\mathbb{R}^d$ 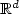 -valued random vector $X \in L^r(\mathbb{P})$
-valued random vector $X \in L^r(\mathbb{P})$ 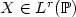 defined in the probability space $(\Omega,\mathcal{A},\mathbb{P})$
defined in the probability space $(\Omega,\mathcal{A},\mathbb{P})$ 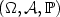 with distribution $\mathbb{P}_{X} = P$
with distribution $\mathbb{P}_{X} = P$ 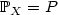 . To be precise, we investigate the Ls -quantization rate of sequences $\alpha_n^{\theta,\mu} = \mu + \theta(\alpha_n-\mu)=\{\mu + \theta(a-\mu), \ a \in \alpha_n \}$
. To be precise, we investigate the Ls -quantization rate of sequences $\alpha_n^{\theta,\mu} = \mu + \theta(\alpha_n-\mu)=\{\mu + \theta(a-\mu), \ a \in \alpha_n \}$ 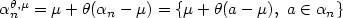 when $\theta \in \mathbb{R}_{+}^{\star}, \mu \in \mathbb{R}, s \in (0,r)$
when $\theta \in \mathbb{R}_{+}^{\star}, \mu \in \mathbb{R}, s \in (0,r)$ 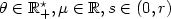 or s ∈ (r, +∞) and $X \in L^s(\mathbb{P})$
or s ∈ (r, +∞) and $X \in L^s(\mathbb{P})$ 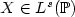 . We show that for a wide family of distributions, one may always find parameters (θ,µ) such that (αnθ,µ)n≥1 is Ls -rate-optimal. For the Gaussian and the exponential distributions we show the existence of a couple (θ*,µ*) such that (αθ*,µ*)n≥1 also satisfies the so-called Ls -empirical measure theorem. Our conjecture, confirmed by numerical experiments, is that such sequences are asymptotically Ls -optimal. In both cases the sequence (αθ*,µ*)n≥1 is incredibly close to Ls -optimality. However we show (see Rem. 5.4) that this last sequence is not Ls -optimal (e.g. when s = 2, r = 1) for the exponential distribution.
. We show that for a wide family of distributions, one may always find parameters (θ,µ) such that (αnθ,µ)n≥1 is Ls -rate-optimal. For the Gaussian and the exponential distributions we show the existence of a couple (θ*,µ*) such that (αθ*,µ*)n≥1 also satisfies the so-called Ls -empirical measure theorem. Our conjecture, confirmed by numerical experiments, is that such sequences are asymptotically Ls -optimal. In both cases the sequence (αθ*,µ*)n≥1 is incredibly close to Ls -optimality. However we show (see Rem. 5.4) that this last sequence is not Ls -optimal (e.g. when s = 2, r = 1) for the exponential distribution.