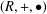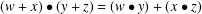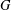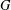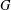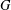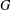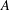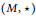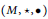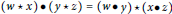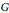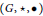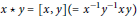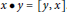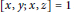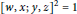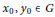An interchange ring, (R,+,\bullet )$(R,+,\bullet )$ , is an abelian group with a second binary operation defined so that the interchange law (w+x)\bullet (y+z)=(w\bullet y)+(x\bullet z)$(w+x)\bullet (y+z)=(w\bullet y)+(x\bullet z)$ holds. An interchange near ring is the same structure based on a group which may not be abelian. It is shown that each interchange (near) ring based on a group G$G$ is formed from a pair of endomorphisms of G$G$ whose images commute, and that all interchange (near) rings based on G$G$ can be characterized in this manner. To obtain an associative interchange ring, the endomorphisms must be commuting idempotents in the endomorphism semigroup of G$G$ . For G$G$ a finite abelian group, we develop a group-theoretic analogue of the simultaneous diagonalization of idempotent linear operators and show that pairs of endomorphisms which yield associative interchange rings can be diagonalized and then put into a canonical form. A best possible upper bound of 4^{r}$4^{r}$ can be given for the number of distinct isomorphism classes of associative interchange rings based on a finite abelian group A$A$ which is a direct sum of r$r$ cyclic groups of prime power order. If A$A$ is a direct sum of r$r$ copies of the same cyclic group of prime power order, we show that there are exactly {\textstyle \frac{1}{6}}(r+1)(r+2)(r+3)${\textstyle \frac{1}{6}}(r+1)(r+2)(r+3)$ distinct isomorphism classes of associative interchange rings based on A$A$ . Several examples are given and further comments are made about the general theory of interchange rings.

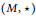A magma\left( M,\star \right)$\left( M,\star \right)$ is a nonempty set with a binary operation. A double magma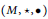\left( M,\star ,\bullet \right)$\left( M,\star ,\bullet \right)$ is a nonempty set with two binary operations satisfying the interchange law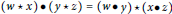\left( w\star x \right)\bullet \left( y\star z \right)=\left( w\bullet y \right)\star \left( x\bullet z \right)$\left( w\star x \right)\bullet \left( y\star z \right)=\left( w\bullet y \right)\star \left( x\bullet z \right)$. We call a double magma proper if the two operations are distinct, and commutative if the operations are commutative. A double semigroup, first introduced by Kock, is a double magma for which both operations are associative. Given a non-trivial group 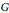G$G$ we define a system of two magma 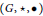\left( G,\star ,\bullet \right)$\left( G,\star ,\bullet \right)$ using the commutator operations 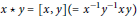x\star y=\left[ x,y \right]\left( ={{x}^{-1}}{{y}^{-1}}xy \right)$x\star y=\left[ x,y \right]\left( ={{x}^{-1}}{{y}^{-1}}xy \right)$ and 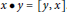x\bullet y=\left[ y,x \right]$x\bullet y=\left[ y,x \right]$. We show that 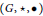\left( G,\star ,\bullet \right)$\left( G,\star ,\bullet \right)$ is a double magma if and only if 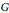G$G$ satisfies the commutator laws 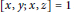\left[ x,y;x,z \right]=1$\left[ x,y;x,z \right]=1$ and 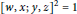{{\left[ w,x;y,z \right]}^{2}}=1${{\left[ w,x;y,z \right]}^{2}}=1$. We note that the first law defines the class of 3-metabelian groups. If both these laws hold in 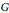G$G$, the double magma is proper if and only if there exist 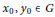{{x}_{0}},{{y}_{0}}\in G${{x}_{0}},{{y}_{0}}\in G$ for which {{\left[ {{x}_{0}},{{y}_{0}} \right]}^{2}}\ne 1${{\left[ {{x}_{0}},{{y}_{0}} \right]}^{2}}\ne 1$. This double magma is a double semigroup if and only if 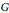G$G$ is nilpotent of class two. We construct a specific example of a proper double semigroup based on the dihedral group of order 16. In addition, we comment on a similar construction for rings using Lie commutators.