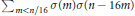1 results
The Convolution Sum Σm<n/16σ(m)σ(n – 16m)
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 1 / 01 March 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-14
- Print publication:
- 01 March 2008
-
- Article
-
- You have access
- Export citation
-
The convolution sum
$\sum{_{m<n/16}\,\sigma (m)\sigma (n\,}-16m)$
is evaluated for all 
$n\,\in \,\mathbb{N}$. This evaluation is used to determine the number of representations of 
$n$ by the quadratic form
$x_{1}^{2}\,+\,x_{2}^{2}\,+\,x_{3}^{2}\,+\,x_{4}^{2}\,+\,4x_{5}^{2}\,+\,4x_{6}^{2}\,+\,4x_{7}^{2}\,+\,4x_{8}^{2}$.
