1 results
Covering Discs in Minkowski Planes
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 3 / 01 September 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 424-434
- Print publication:
- 01 September 2009
-
- Article
-
- You have access
- Export citation
-
We investigate the following version of the circle covering problem in strictly convex (normed or) Minkowski planes: to cover a circle of largest possible diameter by
$k$ unit circles. In particular, we study the cases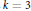 
$k\,=\,3$, 
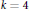$k\,=\,4$, and 
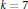$k\,=\,7$. For 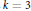$k\,=\,3$ and 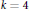$k\,=\,4$, the diameters under consideration are described in terms of side-lengths and circumradii of certain inscribed regular triangles or quadrangles. This yields also simple explanations of geometric meanings that the corresponding homothety ratios have. It turns out that basic notions from Minkowski geometry play an essential role in our proofs, namely Minkowskian bisectors, 
$d$-segments, and the monotonicity lemma.
