The cyclic shift of a language L, defined as SHIFT(L) = {vu | uv ∈ L}, is an operation known to preserve both regularity and context-freeness. Its descriptional complexity has been addressed in Maslov's pioneering paper on the state complexity of regular language operations [Soviet Math. Dokl.11 (1970) 1373–1375], where a high lower bound for partial DFAs using a growing alphabet was given. We improve this result by using a fixed 4-letter alphabet, obtaining a lower bound (n-1)! . 2(n-1)(n-2), which shows that the state complexity of cyclic shift is 2n2+ nlogn - O(n) for alphabets with at least 4 letters. For 2- and 3-letter alphabets, we prove $2^{\Theta(n^2)}$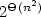 state complexity. We also establish a tight 2n2+1 lower bound for the nondeterministic state complexity of this operation using a binary alphabet.