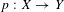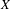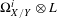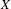1 results
ALGEBRAIC FIBER SPACES AND CURVATURE OF HIGHER DIRECT IMAGES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 03 September 2020, pp. 973-1028
- Print publication:
- May 2022
-
- Article
- Export citation