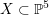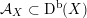2 results
The K3 category of a cubic fourfold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 586-620
- Print publication:
- March 2017
-
- Article
- Export citation
The period map for cubic threefolds
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 4 / July 2007
- Published online by Cambridge University Press:
- 17 July 2007, pp. 1037-1049
- Print publication:
- July 2007
-
- Article
-
- You have access
- Export citation