We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider the hard-core model on a finite square grid graph with stochastic Glauber dynamics parametrized by the inverse temperature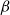 
$\beta$. We investigate how the transition between its two maximum-occupancy configurations takes place in the low-temperature regime 
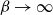$\beta \to \infty$ in the case of periodic boundary conditions. The hard-core constraints and the grid symmetry make the structure of the critical configurations for this transition, also known as essential saddles, very rich and complex. We provide a comprehensive geometrical characterization of these configurations that together constitute a bottleneck for the Glauber dynamics in the low-temperature limit. In particular, we develop a novel isoperimetric inequality for hard-core configurations with a fixed number of particles and show how the essential saddles are characterized not only by the number of particles but also their geometry.
