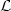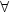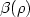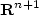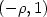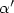Let {\cal L} 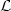 (x,u,∇ u) be a Lagrangian periodic of period 1 in x 1,...,x n ,u. We shall study the non self intersectingfunctions u: R n {\to}
(x,u,∇ u) be a Lagrangian periodic of period 1 in x 1,...,x n ,u. We shall study the non self intersectingfunctions u: R n {\to}  R minimizing {\cal L}
R minimizing {\cal L} 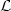 ; non self intersecting means that, if u(x 0 + k) + j = u(x 0) for some x 0∈R n and (k , j) ∈Z n × Z, then u(x) = u(x + k) + j \;\forall
; non self intersecting means that, if u(x 0 + k) + j = u(x 0) for some x 0∈R n and (k , j) ∈Z n × Z, then u(x) = u(x + k) + j \;\forall 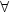 x. Moser has shown that each of these functions is at finite distance from a plane u = ρ \cdot
x. Moser has shown that each of these functions is at finite distance from a plane u = ρ \cdot  x and thus has an average slope ρ; moreover, Senn has proven that it is possible to define the average action of u, which is usually called \beta(\rho)
x and thus has an average slope ρ; moreover, Senn has proven that it is possible to define the average action of u, which is usually called \beta(\rho) 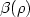 since it only depends on the slope of u.Aubry and Senn have noticed a connection between \beta(\rho)
since it only depends on the slope of u.Aubry and Senn have noticed a connection between \beta(\rho) 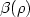 and the theory of crystals in {\bf R}^{n+1}
and the theory of crystals in {\bf R}^{n+1} 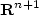 , interpreting \beta(\rho)
, interpreting \beta(\rho) 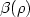 as the energy per area of a crystal face normal to (-\rho,1)
as the energy per area of a crystal face normal to (-\rho,1) 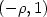 . The polar of β is usually called -α; Senn has shown that α is C 1 and that the dimension of the flat of α which contains c depends only on the “rational space” of \alpha^\prime
. The polar of β is usually called -α; Senn has shown that α is C 1 and that the dimension of the flat of α which contains c depends only on the “rational space” of \alpha^\prime 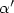 (c). We prove a similar result for the faces (or the faces of the faces, etc.) of the flats of α: they are C 1 and their dimension depends only on the rational space of their normals.
(c). We prove a similar result for the faces (or the faces of the faces, etc.) of the flats of α: they are C 1 and their dimension depends only on the rational space of their normals.