1 results
Regularity and variationality of solutionsto Hamilton-Jacobi equations. Part I: Regularity
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 10 / Issue 3 / July 2004
- Published online by Cambridge University Press:
- 15 June 2004, pp. 426-451
- Print publication:
- July 2004
-
- Article
- Export citation
-
We formulate an Hamilton-Jacobi partial differential equation H( x, D u(x))=0 on a n dimensional manifold M, with assumptions of convexity of H(x, .) and regularity of H (locally in a neighborhood of {H=0} in T*M); we define the “minsol solution” u, a generalized solution; to this end, we view T*Mas a symplectic manifold.The definition of “minsol solution” is suited to proving regularity results about u; in particular, we provein the first part that the closure of the set where u is not regular may be covered by a countable number of $n-1$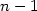
dimensional manifolds, but for a ${{\mathcal H}}^{n-1}$ 
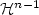negligeable subset.These results can be applied to the cutlocus of a C 2 submanifold of a Finsler manifold.
