We describe a method for constructing explicit algebraic solutions to the sixth Painlevé equation, generalising that of Dubrovin and Mazzocco. There are basically two steps. First we explain how to construct finite braid group orbits of triples of elements of {\rm SL}_2({\rm C}) out of triples of generators of three-dimensional complex reflection groups. (This involves the Fourier–Laplace transform for certain irregular connections.) Then we adapt a result of Jimbo to produce the Painlevé VI solutions. (In particular, this solves a Riemann–Hilbert problem explicitly.)
Each step is illustrated using the complex reflection group associated to Klein's simple group of order 168. This leads to a new algebraic solution with seven branches. We also prove that, unlike the algebraic solutions of Dubrovin and Mazzocco and Hitchin, this solution is not equivalent to any solution coming from a finite subgroup of {\rm SL}_2({\rm C}).
The results of this paper also yield a simple proof of a recent theorem of Inaba, Iwasaki and Saito on the action of Okamoto's affine {\rm D}_4 symmetry group as well as the correct connection formulae for generic Painlevé VI equations.
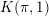 $K(\unicode[STIX]{x1D70B},1)$-problem for restrictions of complex reflection arrangements
$K(\unicode[STIX]{x1D70B},1)$-problem for restrictions of complex reflection arrangements

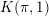
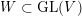
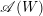
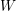
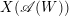
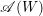
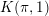
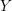
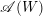
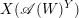
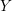
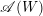
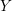
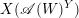
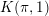
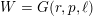
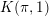
 for the rational Cherednik algebra of type
for the rational Cherednik algebra of type 