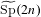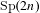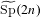1 results
SPECTRAL TRANSFER FOR METAPLECTIC GROUPS. I. LOCAL CHARACTER RELATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 07 December 2016, pp. 25-123
- Print publication:
- January 2019
-
- Article
- Export citation
-
Let
$\widetilde{\text{Sp}}(2n)$ be the metaplectic covering of 
$\text{Sp}(2n)$ over a local field of characteristic zero. The core of the theory of endoscopy for 
$\widetilde{\text{Sp}}(2n)$ is the geometric transfer of orbital integrals to its elliptic endoscopic groups. The dual of this map, called the spectral transfer, is expected to yield endoscopic character relations which should reveal the internal structure of 
$L$-packets. As a first step, we characterize the image of the collective geometric transfer in the non-archimedean case, then reduce the spectral transfer to the case of cuspidal test functions by using a simple stable trace formula. In the archimedean case, we establish the character relations and determine the spectral transfer factors by rephrasing the works by Adams and Renard.
