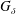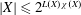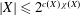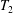We present a result about 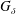 $G_{\unicode[STIX]{x1D6FF}}$ covers of a Hausdorff space that implies various known cardinal inequalities, including the following two fundamental results in the theory of cardinal invariants in topology:
$G_{\unicode[STIX]{x1D6FF}}$ covers of a Hausdorff space that implies various known cardinal inequalities, including the following two fundamental results in the theory of cardinal invariants in topology: 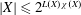 $|X|\leqslant 2^{L(X)\unicode[STIX]{x1D712}(X)}$ (Arhangel’skiĭ) and
$|X|\leqslant 2^{L(X)\unicode[STIX]{x1D712}(X)}$ (Arhangel’skiĭ) and 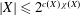 $|X|\leqslant 2^{c(X)\unicode[STIX]{x1D712}(X)}$ (Hajnal–Juhász). This solves a question that goes back to Bell, Ginsburg and Woods’s 1978 paper (M. Bell, J.N. Ginsburg and R.G. Woods, Cardinal inequalities for topological spaces involving the weak Lindelöf number, Pacific J. Math. 79(1978), 37–45) and is mentioned in Hodel’s survey on Arhangel’skiĭ’s Theorem (R. Hodel, Arhangel’skii’s solution to Alexandroff’s problem: A survey, Topology Appl. 153(2006), 2199–2217).
$|X|\leqslant 2^{c(X)\unicode[STIX]{x1D712}(X)}$ (Hajnal–Juhász). This solves a question that goes back to Bell, Ginsburg and Woods’s 1978 paper (M. Bell, J.N. Ginsburg and R.G. Woods, Cardinal inequalities for topological spaces involving the weak Lindelöf number, Pacific J. Math. 79(1978), 37–45) and is mentioned in Hodel’s survey on Arhangel’skiĭ’s Theorem (R. Hodel, Arhangel’skii’s solution to Alexandroff’s problem: A survey, Topology Appl. 153(2006), 2199–2217).
In contrast to previous attempts, we do not need any separation axiom beyond 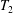 $T_{2}$.
$T_{2}$.