Let 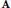 $\mathbf{A}$ be a density matrix in
$\mathbf{A}$ be a density matrix in  ${{\mathbb{M}}_{m}}\,\otimes \,{{\mathbb{M}}_{n}}$. Audenaert [J. Math. Phys. 48(2007) 083507] proved an inequality for Schatten
${{\mathbb{M}}_{m}}\,\otimes \,{{\mathbb{M}}_{n}}$. Audenaert [J. Math. Phys. 48(2007) 083507] proved an inequality for Schatten 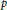 $p$-norms:
$p$-norms:
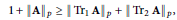 $$1\,+\,||\mathbf{A}|{{|}_{p}}\,\ge \,{{\left\| \text{T}{{\text{r}}_{1}}\,\mathbf{A} \right\|}_{p}}\,+\,||\text{T}{{\text{r}}_{2}}\,\mathbf{A}|{{|}_{p}},$$
$$1\,+\,||\mathbf{A}|{{|}_{p}}\,\ge \,{{\left\| \text{T}{{\text{r}}_{1}}\,\mathbf{A} \right\|}_{p}}\,+\,||\text{T}{{\text{r}}_{2}}\,\mathbf{A}|{{|}_{p}},$$
where  $\text{T}{{\text{r}}_{1}}$ and
$\text{T}{{\text{r}}_{1}}$ and  $\text{T}{{\text{r}}_{2}}$ stand for the first and second partial trace, respectively. As an analogue of his result, we prove a determinantal inequality
$\text{T}{{\text{r}}_{2}}$ stand for the first and second partial trace, respectively. As an analogue of his result, we prove a determinantal inequality
 $$1\,+\,\det \,\mathbf{A}\,\ge \,\det {{\left( \text{T}{{\text{r}}_{1}}\mathbf{A} \right)}^{m}}\,+\,\det {{\left( \text{T}{{\text{r}}_{2}}\mathbf{A} \right)}^{2}}.$$
$$1\,+\,\det \,\mathbf{A}\,\ge \,\det {{\left( \text{T}{{\text{r}}_{1}}\mathbf{A} \right)}^{m}}\,+\,\det {{\left( \text{T}{{\text{r}}_{2}}\mathbf{A} \right)}^{2}}.$$