In this paper we establish the existence of a positive solution
for an asymptotically linear elliptic problem on $\xR^N$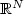 . The main
difficulties to overcome are the lack of a priori bounds for
Palais–Smale sequences and a lack of compactness as the domain is
unbounded. For the first one we make use of techniques introduced
by Lions in his work on concentration compactness. For the
second we show how the fact that the “Problem at infinity” is
autonomous, in contrast to just periodic, can be used in order to
regain compactness.
. The main
difficulties to overcome are the lack of a priori bounds for
Palais–Smale sequences and a lack of compactness as the domain is
unbounded. For the first one we make use of techniques introduced
by Lions in his work on concentration compactness. For the
second we show how the fact that the “Problem at infinity” is
autonomous, in contrast to just periodic, can be used in order to
regain compactness.
 autonomous at infinity
autonomous at infinity