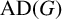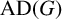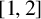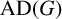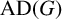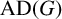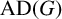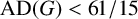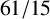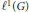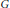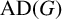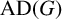For a finite group G, let $\operatorname { {AD}}(G)$ denote the Fourier norm of the antidiagonal in $G\times G$. The author showed recently in [‘An explicit minorant for the amenability constant of the Fourier algebra’, Int. Math. Res. Not. IMRN 2023 (2023), 19390–19430] that $\operatorname { {AD}}(G)$ coincides with the amenability constant of the Fourier algebra of G and is equal to the normalized sum of the cubes of the character degrees of G. Motivated by a gap result for amenability constants from Johnson [‘Non-amenability of the Fourier algebra of a compact group’, J. Lond. Math. Soc. (2) 50 (1994), 361–374], we determine exactly which numbers in the interval 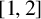$[1,2]$ arise as values of 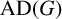$\operatorname { {AD}}(G)$. As a by-product, we show that the set of values of 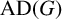$\operatorname { {AD}}(G)$ does not contain all its limit points. Some other calculations or bounds for 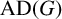$\operatorname { {AD}}(G)$ are given for familiar classes of finite groups. We also indicate a connection between 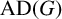$\operatorname { {AD}}(G)$ and the commuting probability of G, and use this to show that every finite group G satisfying 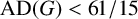$\operatorname { {AD}}(G)< {61}/{15}$ must be solvable; here, the value 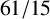${61}/{15}$ is the best possible.

We calculate the exact amenability constant of the centre of ${{\ell }^{1}}\left( G \right)$ when $G$ is a finite group and is either dihedral, extraspecial, or Frobenius with abelian complement and kernel. This is done using a formula that applies to all finite groups with two character degrees. In passing, we answer in the negative a question raised in work of the third author with Azimifard and Spronk.