We show that spaces of Colombeau generalized functions with smooth parameter dependence are isomorphic to those with continuous parametrization. Based on this result we initiate a systematic study of algebraic properties of the ring 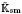 of generalized numbers in this unified setting. In particular, we investigate the ring and order structure of
of generalized numbers in this unified setting. In particular, we investigate the ring and order structure of 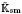 and establish some properties of its ideals.
and establish some properties of its ideals.