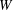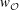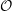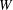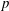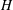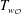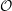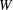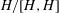Given an affine Coxeter group W, the corresponding Shi arrangement is a refinement of the corresponding Coxeter hyperplane arrangements that was introduced by Shi to study Kazhdan–Lusztig cells for W. Shi showed that each region of the Shi arrangement contains exactly one element of minimal length in W. Low elements in W were introduced to study the word problem of the corresponding Artin–Tits (braid) group and turns out to produce automata to study the combinatorics of reduced words in W. In this article, we show, in the case of an affine Coxeter group, that the set of minimal length elements of the regions in the Shi arrangement is precisely the set of low elements, settling a conjecture of Dyer and the second author in this case. As a by-product of our proof, we show that the descent walls – the walls that separate a region from the fundamental alcove – of any region in the Shi arrangement are precisely the descent walls of the alcove of its corresponding low element.

Let 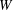$W$ be an extended affine Weyl group. We prove that the minimal length elements 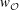$w_{{\mathcal{O}}}$ of any conjugacy class 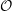${\mathcal{O}}$ of 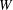$W$ satisfy some nice properties, generalizing results of Geck and Pfeiffer [On the irreducible characters of Hecke algebras, Adv. Math. 102 (1993), 79–94] on finite Weyl groups. We also study a special class of conjugacy classes, the straight conjugacy classes. These conjugacy classes are in a natural bijection with the Frobenius-twisted conjugacy classes of some 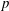$p$-adic group and satisfy additional interesting properties. Furthermore, we discuss some applications to the affine Hecke algebra 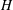$H$. We prove that 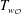$T_{w_{{\mathcal{O}}}}$, where 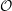${\mathcal{O}}$ ranges over all the conjugacy classes of 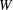$W$, forms a basis of the cocenter 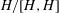$H/[H,H]$. We also introduce the class polynomials, which play a crucial role in the study of affine Deligne–Lusztig varieties He [Geometric and cohomological properties of affine Deligne–Lusztig varieties, Ann. of Math. (2) 179 (2014), 367–404].

We define certain extensions of affine Weyl groups (distinct from these considered by K. Saito [S1] in the theory of extended affine root systems), prove an analogue of Chevalley Theorem for their invariants, and construct a Frobenius structure on their orbit spaces. This produces solutions $F(t_1, …, t_n)$ of WDVV equations of associativity polynomial in $t_1, …, t_n-1$, exp $t_n$.

Let $G$ be a complex, semisimple, simply connected algebraic group with Lie algebra ${\frak g}$. We extend scalars to the power series field in one variable ${\rm C}((\pi))$, and consider the space of Iwahori subalgebras containing a fixed nil-elliptic element of ${\frak g} \otimes {\rm C}((\pi))$, i.e. fixed point varieties on the full affine flag manifold. We define representations of the affine Weyl group in the homology of these varieties, generalizing Kazhdan and Lusztig's topological construction of Springer's representations to the affine context.