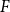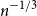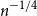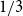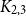1 results
Turán problems in pseudorandom graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 29 April 2024, pp. 583-596
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
Given a graph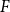
$F$, we consider the problem of determining the densest possible pseudorandom graph that contains no copy of 
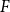$F$. We provide an embedding procedure that improves a general result of Conlon, Fox, and Zhao which gives an upper bound on the density. In particular, our result implies that optimally pseudorandom graphs with density greater than 
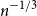$n^{-1/3}$ must contain a copy of the Peterson graph, while the previous best result gives the bound 
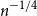$n^{-1/4}$. Moreover, we conjecture that the exponent 
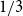$1/3$ in our bound is tight. We also construct the densest known pseudorandom 
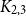$K_{2,3}$-free graphs that are also triangle-free. Finally, we give a different proof for the densest known construction of clique-free pseudorandom graphs due to Bishnoi, Ihringer, and Pepe that they have no large clique.
