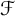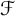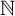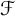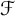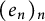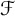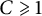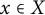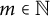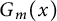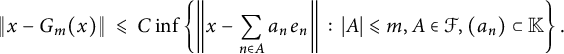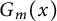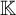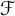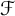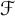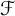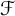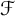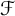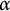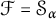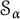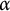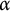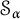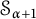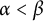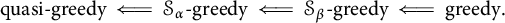Let 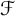 $\mathcal {F}$ be a hereditary collection of finite subsets of
$\mathcal {F}$ be a hereditary collection of finite subsets of 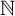 $\mathbb {N}$. In this paper, we introduce and characterize
$\mathbb {N}$. In this paper, we introduce and characterize 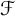 $\mathcal {F}$-(almost) greedy bases. Given such a family
$\mathcal {F}$-(almost) greedy bases. Given such a family 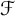 $\mathcal {F}$, a basis
$\mathcal {F}$, a basis 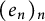 $(e_n)_n$ for a Banach space X is called
$(e_n)_n$ for a Banach space X is called 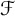 $\mathcal {F}$-greedy if there is a constant
$\mathcal {F}$-greedy if there is a constant 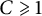 $C\geqslant 1$ such that for each
$C\geqslant 1$ such that for each 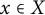 $x\in X$,
$x\in X$, 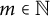 $m \in \mathbb {N}$, and
$m \in \mathbb {N}$, and 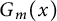 $G_m(x)$, we have
$G_m(x)$, we have 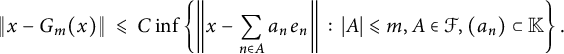 $$ \begin{align*} \|x - G_m(x)\|\ \leqslant\ C \inf\left\{\left\|x-\sum_{n\in A}a_ne_n\right\|\,:\, |A|\leqslant m, A\in \mathcal{F}, (a_n)\subset \mathbb{K}\right\}. \end{align*} $$
$$ \begin{align*} \|x - G_m(x)\|\ \leqslant\ C \inf\left\{\left\|x-\sum_{n\in A}a_ne_n\right\|\,:\, |A|\leqslant m, A\in \mathcal{F}, (a_n)\subset \mathbb{K}\right\}. \end{align*} $$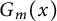 $G_m(x)$ is a greedy sum of x of order m, and
$G_m(x)$ is a greedy sum of x of order m, and 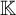 $\mathbb {K}$ is the scalar field. From the definition, any
$\mathbb {K}$ is the scalar field. From the definition, any 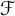 $\mathcal {F}$-greedy basis is quasi-greedy, and so the notion of being
$\mathcal {F}$-greedy basis is quasi-greedy, and so the notion of being 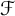 $\mathcal {F}$-greedy lies between being greedy and being quasi-greedy. We characterize
$\mathcal {F}$-greedy lies between being greedy and being quasi-greedy. We characterize 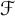 $\mathcal {F}$-greedy bases as being
$\mathcal {F}$-greedy bases as being 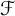 $\mathcal {F}$-unconditional,
$\mathcal {F}$-unconditional, 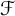 $\mathcal {F}$-disjoint democratic, and quasi-greedy, thus generalizing the well-known characterization of greedy bases by Konyagin and Temlyakov. We also prove a similar characterization for
$\mathcal {F}$-disjoint democratic, and quasi-greedy, thus generalizing the well-known characterization of greedy bases by Konyagin and Temlyakov. We also prove a similar characterization for 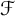 $\mathcal {F}$-almost greedy bases.
$\mathcal {F}$-almost greedy bases.
Furthermore, we provide several examples of bases that are nontrivially 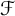 $\mathcal {F}$-greedy. For a countable ordinal
$\mathcal {F}$-greedy. For a countable ordinal 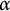 $\alpha $, we consider the case
$\alpha $, we consider the case 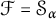 $\mathcal {F}=\mathcal {S}_{\alpha }$, where
$\mathcal {F}=\mathcal {S}_{\alpha }$, where 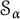 $\mathcal {S}_{\alpha }$ is the Schreier family of order
$\mathcal {S}_{\alpha }$ is the Schreier family of order 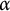 $\alpha $. We show that for each
$\alpha $. We show that for each 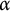 $\alpha $, there is a basis that is
$\alpha $, there is a basis that is 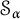 $\mathcal {S}_{\alpha }$-greedy but is not
$\mathcal {S}_{\alpha }$-greedy but is not 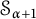 $\mathcal {S}_{\alpha +1}$-greedy. In other words, we prove that none of the following implications can be reversed: for two countable ordinals
$\mathcal {S}_{\alpha +1}$-greedy. In other words, we prove that none of the following implications can be reversed: for two countable ordinals 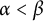 $\alpha < \beta $,
$\alpha < \beta $, 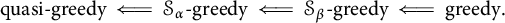 $$ \begin{align*} \mbox{quasi-greedy}\ \Longleftarrow\ \mathcal{S}_{\alpha}\mbox{-greedy}\ \Longleftarrow\ \mathcal{S}_{\beta}\mbox{-greedy}\ \Longleftarrow\ \mbox{greedy}. \end{align*} $$
$$ \begin{align*} \mbox{quasi-greedy}\ \Longleftarrow\ \mathcal{S}_{\alpha}\mbox{-greedy}\ \Longleftarrow\ \mathcal{S}_{\beta}\mbox{-greedy}\ \Longleftarrow\ \mbox{greedy}. \end{align*} $$
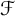 $\mathcal {F}$-(almost) greedy bases
$\mathcal {F}$-(almost) greedy bases