We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let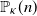 
$\mathbb{P}_\kappa(n)$ be the probability that n points 
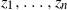$z_1,\ldots,z_n$ picked uniformly and independently in 
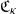$\mathfrak{C}_\kappa$, a regular 
$\kappa$-gon with area 1, are in convex position, that is, form the vertex set of a convex polygon. In this paper, we compute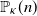 
$\mathbb{P}_\kappa(n)$ up to asymptotic equivalence, as 
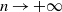$n\to+\infty$, for all 
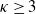$\kappa\geq 3$, which improves on a famous result of Bárány (Ann. Prob. 27, 1999). The second purpose of this paper is to establish a limit theorem which describes the fluctuations around the limit shape of an n-tuple of points in convex position when 
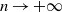$n\to+\infty$. Finally, we give an asymptotically exact algorithm for the random generation of 
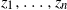$z_1,\ldots,z_n$, conditioned to be in convex position in 
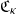$\mathfrak{C}_\kappa$.
