We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
On the half space Rn × R+, it has been known that harmonic Bergman space bp can contain a positive function only if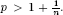 
. Thus, for 
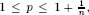, Poisson integrals can be bp-functions only by means of their boundary cancellation properties. In this paper, we describe what those cancellation properties explicitly are. Also, given such cancellation properties, we obtain weighted norm inequalities for Poisson integrals. As a consequence, under weighted integrability condition given by our weighted norm inequalities, we show that our cancellation properties are equivalent to the bp-containment of Poisson integrals for p under consideration. Our results are sharp in the sense that orders of our weights cannot be improved.
