3 results
Limiting Distributions for a Class Of Diminishing Urn Models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 87-116
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Card Counting in Continuous Time
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 184-198
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
On the fundamental theorem of card counting, with application to the game of trente et quarante
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 90-107
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation

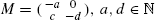 and
and 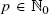 . We determine limiting distributions by obtaining a precise recursive description of the moments of the considered random variables, which allows us to deduce asymptotic expansions of the moments. In particular, we obtain limiting distributions for the pills problem
. We determine limiting distributions by obtaining a precise recursive description of the moments of the considered random variables, which allows us to deduce asymptotic expansions of the moments. In particular, we obtain limiting distributions for the pills problem 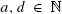 and
and 