1 results
Integer-valued branching processes with immigration
-
- Journal:
- Advances in Applied Probability / Volume 15 / Issue 4 / December 1983
- Published online by Cambridge University Press:
- 01 July 2016, pp. 713-725
- Print publication:
- December 1983
-
- Article
- Export citation
-
The notion of self-decomposability for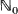
-valued random variables as introduced by Steutel and van Harn [10] and its generalization by van Harn, Steutel and Vervaat [5], are used to study the limiting behaviour of continuous-time Markov branching processes with immigration. This behaviour provides analogues to the behaviour of sequences of random variables obeying a certain difference equation as studied by Vervaat [12] and their continuous-time counterpart considered by Wolfe [13]. An application in queueing theory is indicated. Furthermore, discrete-state analogues are given for results on stability in the processes studied by Wolfe, and for results on self-decomposability in supercritical branching processes by Yamazato [14].
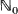-valued random variables as introduced by Steutel and van Harn [10] and its generalization by van Harn, Steutel and Vervaat [5], are used to study the limiting behaviour of continuous-time Markov branching processes with immigration. This behaviour provides analogues to the behaviour of sequences of random variables obeying a certain difference equation as studied by Vervaat [12] and their continuous-time counterpart considered by Wolfe [13]. An application in queueing theory is indicated. Furthermore, discrete-state analogues are given for results on stability in the processes studied by Wolfe, and for results on self-decomposability in supercritical branching processes by Yamazato [14].