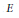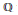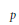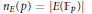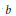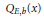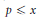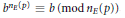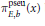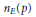1 results
Pseudoprime Reductions of Elliptic Curves
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 1 / 01 February 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 81-101
- Print publication:
- 01 February 2012
-
- Article
-
- You have access
- Export citation
-
Let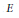
$E$ be an elliptic curve over 
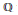$\mathbb{Q}$ without complex multiplication, and for each prime 
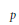$p$ of good reduction, let 
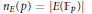${{n}_{E}}(p)\,=\,\left| E\left( {{\mathbb{F}}_{p}} \right) \right|$. For any integer 
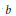$b$, we consider elliptic pseudoprimes to the base 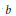$b$. More precisely, let 
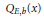${{Q}_{E,B}}(x)$ be the number of primes 
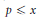$p\le x$ such that 
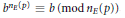${{b}^{{{n}_{E}}(p)}}\,\equiv \,b\left( \bmod \,{{n}_{E}}\left( p \right) \right)$, and let 
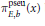$\pi _{E,b}^{\text{pseu}}(x)$ be the number of compositive
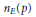${{n}_{E}}(p)$ such that 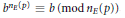${{b}^{{{n}_{E}}(p)}}\,\equiv \,b\left( \bmod \,{{n}_{E}}\left( p \right) \right)$ (also called elliptic curve pseudoprimes). Motivated by cryptography applications, we address the problem of finding upper bounds for 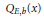${{Q}_{E,B}}(x)$ and 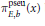$\pi _{E,b}^{\text{pseu}}(x)$, generalising some of the literature for the classical pseudoprimes to this new setting.
