18 results
Estimation of Effect Heterogeneity in Rare Events Meta-Analysis
-
- Journal:
- Psychometrika / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 01 January 2025, pp. 1081-1102
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Explaining Recruitment to Extremism: A Bayesian Hierarchical Case–Control Approach
-
- Journal:
- Political Analysis / Volume 32 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 16 November 2023, pp. 256-274
-
- Article
-
- You have access
- HTML
- Export citation
On the relative importance of the hot stove effect and the tendency to rely on small samples
-
- Journal:
- Judgment and Decision Making / Volume 4 / Issue 5 / August 2009
- Published online by Cambridge University Press:
- 01 January 2023, pp. 429-435
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The coexistence of overestimation and underweighting of rare events and the contingent recency effect
-
- Journal:
- Judgment and Decision Making / Volume 4 / Issue 6 / October 2009
- Published online by Cambridge University Press:
- 01 January 2023, pp. 447-460
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Return- and hitting-time distributions of small sets in infinite measure preserving systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 02 January 2019, pp. 2239-2273
- Print publication:
- August 2020
-
- Article
- Export citation
4 - Implementing MLE
- from Part I - Concepts, Theory, and Implementation
-
- Book:
- Maximum Likelihood for Social Science
- Published online:
- 15 November 2018
- Print publication:
- 15 November 2018, pp 79-94
-
- Chapter
- Export citation
Accelerating rare events and building kinetic Monte Carlo models using temperature programmed molecular dynamics
-
- Journal:
- Journal of Materials Research / Volume 33 / Issue 7 / 13 April 2018
- Published online by Cambridge University Press:
- 21 December 2017, pp. 835-846
- Print publication:
- 13 April 2018
-
- Article
- Export citation
A Minimum Action Method with Optimal Linear Time Scaling
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 5 / November 2015
- Published online by Cambridge University Press:
- 23 November 2015, pp. 1352-1379
- Print publication:
- November 2015
-
- Article
- Export citation
Optimization-Based String Method for Finding Minimum Energy Path
-
- Journal:
- Communications in Computational Physics / Volume 14 / Issue 2 / August 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 265-275
- Print publication:
- August 2013
-
- Article
- Export citation
Numerical analysis of parallel replica dynamics
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 5 / September 2013
- Published online by Cambridge University Press:
- 09 July 2013, pp. 1287-1314
- Print publication:
- September 2013
-
- Article
- Export citation
ADVANCES IN CROSS-ENTROPY METHODS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 02 October 2009, pp. 521-522
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Occupancy schemes associated to Yule processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 600-622
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
A unified approach to fast teller queues and ATM
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 758-787
- Print publication:
- September 1999
-
- Article
- Export citation
Simulation of Ruin Probabilities for Subexponential Claims
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 27 / Issue 2 / November 1997
- Published online by Cambridge University Press:
- 29 August 2014, pp. 297-318
- Print publication:
- November 1997
-
- Article
-
- You have access
- Export citation
A note on the point processes of rare events
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 654-663
- Print publication:
- September 1996
-
- Article
- Export citation
Ruin probabilities via local adjustment coefficients
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 736-755
- Print publication:
- September 1995
-
- Article
- Export citation
Non-linear filtering of rare events with large signal-to-noise ratio
-
- Journal:
- Journal of Applied Probability / Volume 24 / Issue 4 / December 1987
- Published online by Cambridge University Press:
- 14 July 2016, pp. 929-948
- Print publication:
- December 1987
-
- Article
- Export citation
Sojourn times, exit times and jitter in multivariate Markov processes
-
- Journal:
- Advances in Applied Probability / Volume 6 / Issue 4 / December 1974
- Published online by Cambridge University Press:
- 01 July 2016, pp. 747-756
- Print publication:
- December 1974
-
- Article
- Export citation

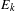
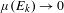



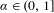

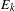
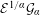
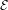
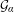
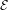
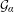

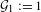
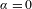
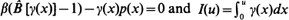 . It is shown that
. It is shown that 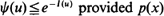 is non-decreasing and that log ψ(u) ≈ –
is non-decreasing and that log ψ(u) ≈ –
