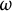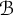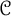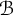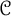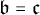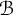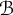We introduce a generalization of sequential compactness using barriers on 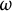\omega $\omega$ extending naturally the notion introduced in [W. Kubiś and P. Szeptycki, On a topological Ramsey theorem, Canad. Math. Bull., 66 (2023), 156–165]. We improve results from [C. Corral and O. Guzmán and C. López-Callejas, High dimensional sequential compactness, Fund. Math.] by building spaces that are 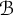{\mathcal {B}}${\mathcal {B}}$-sequentially compact but not 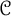{\mathcal {C}}${\mathcal {C}}$-sequentially compact when the barriers 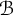{\mathcal {B}}${\mathcal {B}}$ and 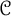{\mathcal {C}}${\mathcal {C}}$ satisfy certain rank assumption which turns out to be equivalent to a Katětov-order assumption. Such examples are constructed under the assumption 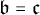{\mathfrak {b}} ={\mathfrak {c}}${\mathfrak {b}} ={\mathfrak {c}}$. We also exhibit some classes of spaces that are 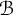{\mathcal {B}}${\mathcal {B}}$-sequentially compact for every barrier 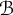{\mathcal {B}}${\mathcal {B}}$, including some classical classes of compact spaces from functional analysis, and as a byproduct, we obtain some results on angelic spaces. Finally, we introduce and compute some cardinal invariants naturally associated to barriers.