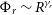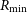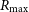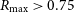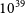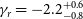Regardless of whether or not all fast radio bursts (FRBs) repeat, those that do form a population with a distribution of rates. This work considers a power-law model of this population, with rate distribution 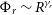 $\Phi_r \sim R^{{\gamma_r}}$ between
$\Phi_r \sim R^{{\gamma_r}}$ between 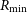 ${R_{\rm min}}$ and
${R_{\rm min}}$ and 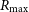 ${R_{\rm max}}$. The zDM code is used to model the probability of detecting this population as either apparently once-off or repeat events as a function of redshift, z, and dispersion measure, DM. I demonstrate that in the nearby Universe, repeating sources can contribute significantly to the total burst rate. This causes an apparent deficit in the total number of observed sources (once-off and repeaters) relative to the distant Universe that will cause a bias in FRB population models. Thus instruments with long exposure times should explicitly take repetition into account when fitting the FRB population. I then fit data from The Canadian Hydrogen Intensity Mapping Experiment (CHIME). The relative number of repeat and apparently once-off FRBs, and their DM, declination, and burst rate distributions, can be well explained by 50–100% of CHIME single FRBs being due to repeaters, with
${R_{\rm max}}$. The zDM code is used to model the probability of detecting this population as either apparently once-off or repeat events as a function of redshift, z, and dispersion measure, DM. I demonstrate that in the nearby Universe, repeating sources can contribute significantly to the total burst rate. This causes an apparent deficit in the total number of observed sources (once-off and repeaters) relative to the distant Universe that will cause a bias in FRB population models. Thus instruments with long exposure times should explicitly take repetition into account when fitting the FRB population. I then fit data from The Canadian Hydrogen Intensity Mapping Experiment (CHIME). The relative number of repeat and apparently once-off FRBs, and their DM, declination, and burst rate distributions, can be well explained by 50–100% of CHIME single FRBs being due to repeaters, with 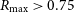 ${R_{\rm max}} > 0.75$ d
${R_{\rm max}} > 0.75$ d $^{-1}$ above
$^{-1}$ above 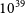 $10^{39}$ erg, and
$10^{39}$ erg, and 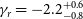 ${{\gamma_r}} = -2.2_{-0.8}^{+0.6}$. This result is surprisingly consistent with follow-up studies of FRBs detected by the Australian Square Kilometre Array Pathfinder (ASKAP). Thus the evidence suggests that CHIME and ASKAP view the same repeating FRB population, which is responsible not just for repeating FRBs, but the majority of apparently once-off bursts. For greater quantitative accuracy, non-Poissonian arrival times, second-order effects in the CHIME response, and a simultaneous fit to the total FRB population parameters, should be treated in more detail in future studies.
${{\gamma_r}} = -2.2_{-0.8}^{+0.6}$. This result is surprisingly consistent with follow-up studies of FRBs detected by the Australian Square Kilometre Array Pathfinder (ASKAP). Thus the evidence suggests that CHIME and ASKAP view the same repeating FRB population, which is responsible not just for repeating FRBs, but the majority of apparently once-off bursts. For greater quantitative accuracy, non-Poissonian arrival times, second-order effects in the CHIME response, and a simultaneous fit to the total FRB population parameters, should be treated in more detail in future studies.