1 results
Mean-square and almost-sure convergence of supercritical age-dependent branching processes
-
- Journal:
- Journal of Applied Probability / Volume 11 / Issue 4 / December 1974
- Published online by Cambridge University Press:
- 14 July 2016, pp. 678-686
- Print publication:
- December 1974
-
- Article
- Export citation

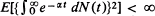 and
and 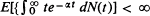 , where
, where 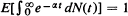 . If the stronger conditions that (Theorem 2)
. If the stronger conditions that (Theorem 2) 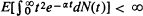 and
and 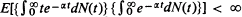 hold also, then the
hold also, then the 