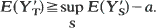1 results
Arret optimal avec contrainte
-
- Journal:
- Advances in Applied Probability / Volume 15 / Issue 4 / December 1983
- Published online by Cambridge University Press:
- 01 July 2016, pp. 798-812
- Print publication:
- December 1983
-
- Article
- Export citation

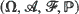 , and a non-negative real
, and a non-negative real