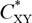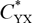1 results
A Derivation of Stiffness and Damping Coefficients for Short Hydrodynamic Journal Bearings with Pseudo-Plastic Lubricants
-
- Journal:
- Journal of Mechanics / Volume 36 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 14 October 2020, pp. 943-953
- Print publication:
- December 2020
-
- Article
- Export citation