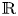Kanai proved powerful results on the stability under quasi-isometries of numerous global properties (including Liouville property) between Riemannian manifolds of bounded geometry. Since his work focuses more on the generality of the spaces considered than on the two-dimensional geometry, Kanai's hypotheses in many cases are not satisfied in the context of Riemann surfaces endowed with the Poincaré metric. In this work we fill that gap for the Liouville property, by proving its stability by quasi-isometries for every Riemann surface (and even Riemannian surfaces with pinched negative curvature). Also, a key result characterizes Riemannian surfaces which are quasi-isometric to $\mathbb {R}$.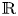

We find approximate solutions (chord–arc curves) for the system of equations of geodesics in Ω∩ℍ for every Denjoy domain Ω, with respect to both the Poincaré and the quasi-hyperbolic metrics. We also prove that these chord–arc curves are uniformly close to the geodesics. As an application of these results, we obtain good estimates for the lengths of simple closed geodesics in any Denjoy domain, and we improve the characterization in a 1999 work by Alvarez et al. on Denjoy domains satisfying the linear isoperimetric inequality.