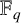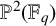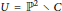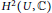6 results
On the monodromy group of the family of smooth quintic plane curves
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 28 November 2024, pp. 163-184
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The analytic classification of plane curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 19 March 2024, pp. 915-944
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
TANGENT-FILLING PLANE CURVES OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 02 May 2023, pp. 301-315
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
ON THE MILNOR MONODROMY OF THE IRREDUCIBLE COMPLEX REFLECTION ARRANGEMENTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 08 November 2017, pp. 1215-1231
- Print publication:
- November 2019
-
- Article
- Export citation
On Hodge Theory of Singular Plane Curves
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 3 / 01 September 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-460
- Print publication:
- 01 September 2016
-
- Article
-
- You have access
- Export citation
Kummer covers and braid monodromy
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 3 / July 2014
- Published online by Cambridge University Press:
- 17 October 2013, pp. 633-670
- Print publication:
- July 2014
-
- Article
- Export citation