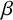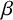2 results
ESTIMATION OF MEAN SQUARED ERRORS OF NON-BINARY A/D ENCODERS THROUGH FREDHOLM DETERMINANTS OF PIECEWISE-LINEAR TRANSFORMATIONS II: GENERAL CASE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 19 March 2025, e14
-
- Article
- Export citation
-
We conduct a theoretical analysis of the performance of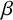
$\beta $-encoders. The 
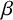$\beta $-encoders are A/D (analogue-to-digital) encoders, the design of which is based on the expansion of real numbers with noninteger radix. For the practical use of such encoders, it is important to have theoretical upper bounds of their errors. We investigate the generating function of the Perron–Frobenius operator of the corresponding one-dimensional map and deduce the invariant measure of it. Using this, we derive an approximate value of the upper bound of the mean squared error of the quantization process of such encoders. We also discuss the results from a numerical viewpoint.
METASTABLE SETS IN OPEN DYNAMICAL SYSTEMS AND SUBSTOCHASTIC MARKOV CHAINS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 08 July 2015, pp. 344-345
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
