Generalized Algebraic Data Types (GADTs) are a syntactic generalization of the usual algebraic data types (ADTs), such as lists, trees, etc. ADTs’ standard initial algebra semantics (IAS) in the category $\mathit{Set}$ of sets justify critical syntactic constructs – such as recursion, pattern matching, and fold – for programming with them. In this paper, we show that semantics for GADTs that specialize to the IAS for ADTs are necessarily unsatisfactory. First, we show that the functorial nature of such semantics for GADTs in $\mathit{Set}$ introduces ghost elements, i.e., elements not writable in syntax. Next, we show how such ghost elements break parametricity. We observe that the situation for GADTs contrasts dramatically with that for ADTs, whose IAS coincides with the parametric model constructed via their Church encodings in System F. Our analysis reveals that the fundamental obstacle to giving a functorial IAS for GADTs is the inherently partial nature of their map functions. We show that this obstacle cannot be overcome by replacing $\mathit{Set}$ with other categories that account for this partiality.

In this paper, we propose a variant of Answer Set Programming (ASP) with evaluable functions that extends their application to sets of objects, something that allows a fully logical treatment of aggregates. Formally, we start from the syntax of First Order Logic with equality and the semantics of Quantified Equilibrium Logic with evaluable functions (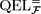${\rm QEL}^=_{\cal F}$). Then, we proceed to incorporate a new kind of logical term, intensional set (a construct commonly used to denote the set of objects characterised by a given formula), and to extend 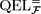${\rm QEL}^=_{\cal F}$ semantics for this new type of expression. In our extended approach, intensional sets can be arbitrarily used as predicate or function arguments or even nested inside other intensional sets, just as regular first-order logical terms. As a result, aggregates can be naturally formed by the application of some evaluable function (count, sum, maximum, etc) to a set of objects expressed as an intensional set. This approach has several advantages. First, while other semantics for aggregates depend on some syntactic transformation (either via a reduct or a formula translation), the 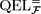${\rm QEL}^=_{\cal F}$ interpretation treats them as regular evaluable functions, providing a compositional semantics and avoiding any kind of syntactic restriction. Second, aggregates can be explicitly defined now within the logical language by the simple addition of formulas that fix their meaning in terms of multiple applications of some (commutative and associative) binary operation. For instance, we can use recursive rules to define sum in terms of integer addition. Last, but not least, we prove that the semantics we obtain for aggregates coincides with the one defined by Gelfond and Zhang for the 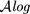${\cal A}\mathit{log}$ language, when we restrict to that syntactic fragment.

Partial functions are common abstractions in formal specification notations such as Z, B and Alloy. Conversely, executable programming languages usually provide little or no support for them. In this paper we propose to add partial functions as a primitive feature to a Constraint Logic Programming (CLP) language, namely {log}. Although partial functions could be programmed on top of {log}, providing them as first-class citizens adds valuable flexibility and generality to the form of set-theoretic formulas that the language can safely deal with. In particular, the paper shows how the {log} constraint solver is naturally extended in order to accommodate for the new primitive constraints dealing with partial functions. Efficiency of the new version is empirically assessed by running a number of non-trivial set-theoretical goals involving partial functions, obtained from specifications written in Z.

In this paper we propose an extension of Answer Set Programming (ASP) to deal with (possibly partial) evaluable functions. To this aim, we start from the most general logical counterpart of ASP, Quantified Equilibrium Logic (QEL), and propose a variant QEL=ℱ where the set of functions is partitioned into Herbrand functions (or constructors) and evaluable functions (or operations). We show how this extension has a direct connection to Scott's Logic of Existence, and introduce several useful derived operators, some of them directly borrowed from Scott's formalisation. Using this general framework for arbitrary theories, we proceed to focus on a syntactic subclass that corresponds to normal logic programs with evaluable functions and equality. We provide a translation of this class into function-free normal programs and consider a safety condition so that the resulting program is also safe, under the usual meaning in ASP. Finally, we also establish a formal comparison to Lin and Wang's approach (FASP) dealing with evaluable total functions.