A large class of traditional graph and data mining algorithms can be concisely expressed in Datalog, and other Logic-based languages, once aggregates are allowed in recursion. In fact, for most BigData algorithms, the difficult semantic issues raised by the use of non-monotonic aggregates in recursion are solved by Pre-Mappability (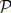 ${\cal P}$ reM), a property that assures that for a program with aggregates in recursion there is an equivalent aggregate-stratified program. In this paper we show that, by bringing together the formal abstract semantics of stratified programs with the efficient operational one of unstratified programs, $\[{\cal P}\]$ reM can also facilitate and improve their parallel execution. We prove that $\[{\cal P}\]$ reM-optimized lock-free and decomposable parallel semi-naive evaluations produce the same results as the single executor programs. Therefore, $\[{\cal P}\]$ reM can be assimilated into the data-parallel computation plans of different distributed systems, irrespective of whether these follow bulk synchronous parallel (BSP) or asynchronous computing models. In addition, we show that non-linear recursive queries can be evaluated using a hybrid stale synchronous parallel (SSP) model on distributed environments. 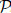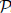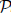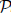After providing a formal correctness proof for the recursive query evaluation with $\[{\cal P}\]$ reM under this relaxed synchronization model, we present experimental evidence of its benefits.