6 results
13 - Creativity: How Noisy Processes Create Novel Structure
- from Part III - Mind
-
- Book:
- Behavioral Network Science
- Published online:
- 08 November 2024
- Print publication:
- 19 December 2024, pp 203-224
-
- Chapter
- Export citation

Percolation in Spatial Networks
- Spatial Network Models Beyond Nearest Neighbours Structures
-
- Published online:
- 15 June 2022
- Print publication:
- 14 July 2022
-
- Element
- Export citation
Spatial dispersion of interstellar civilizations: a probabilistic site percolation model in three dimensions
-
- Journal:
- International Journal of Astrobiology / Volume 12 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 02 October 2012, pp. 45-52
-
- Article
- Export citation
Equality of critical densities in continuum percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 90-104
- Print publication:
- March 1995
-
- Article
- Export citation
Mixed percolation on the square lattice
-
- Journal:
- Journal of Applied Probability / Volume 21 / Issue 2 / June 1984
- Published online by Cambridge University Press:
- 14 July 2016, pp. 247-259
- Print publication:
- June 1984
-
- Article
- Export citation
Bond percolation on honeycomb and triangular lattices
-
- Journal:
- Advances in Applied Probability / Volume 13 / Issue 2 / June 1981
- Published online by Cambridge University Press:
- 01 July 2016, pp. 298-313
- Print publication:
- June 1981
-
- Article
- Export citation

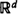 with density ρ, and add the origin as an extra point. Now connect any two points
with density ρ, and add the origin as an extra point. Now connect any two points 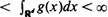 , then the two critical densities are non-trivial, i.e. bounded away from 0 and ∞. It is also known that if
, then the two critical densities are non-trivial, i.e. bounded away from 0 and ∞. It is also known that if 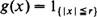 , for some
, for some 