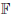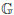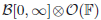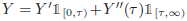Let \hbox{$\mathbb{F}^{}_{}$}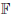$F_{}^{}$ be a filtration and τ be a random time. Let \hbox{$\mathbb{G}^{}_{}$}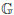$G_{}^{}$ be the progressive enlargement of \hbox{$\mathbb{F}^{}_{}$}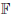$F_{}^{}$ with τ. We study the following formula, called the optional splitting formula: For any \hbox{$\mathbb{G}^{}_{}$}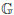$G_{}^{}$-optional process Y, there exists an \hbox{$\mathbb{F}^{}_{}$}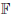$F_{}^{}$-optional process Y′ and a function Y′′ defined on [0,∞] × (ℝ+ × Ω) being \hbox{$\mathcal{B}[0,\infty]\otimes\mathcal{O}(\mathbb{F}^{}_{})$}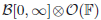$\mathrm{ℬ}\mathrm{\left[}\mathrm{0}\mathit{,}\mathrm{\infty }\mathrm{\right]}\mathrm{\otimes }\mathrm{𝒪}\mathrm{\left(}{F}_{}^{}\mathrm{\right)}$ measurable, such that \hbox{$Y=Y'\mathds{1}^{}_{[0,\tau)}+Y''(\tau)\mathbb{1}^{}_{[\tau,\infty)}.$}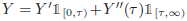$\mathit{Y}\mathrm{=}{\mathit{Y}}^{\mathrm{\prime }}{1}_{\mathrm{\left[}\mathrm{0}\mathit{,\tau }\mathrm{\right)}}^{}\mathrm{+}{\mathit{Y}}^{\mathrm{\prime \prime }}\mathrm{\left(}\mathit{\tau }\mathrm{\right)}{1}_{\mathrm{\left[}\mathit{\tau ,}\mathrm{\infty }\mathrm{\right)}}^{}\mathit{.}$ (This formula can also be formulated for multiple random times τ1,...,τk). We are interested in this formula because of its fundamental role in many recent papers on credit risk modeling, and also because of the fact that its validity is limited in scope and this limitation is not sufficiently underlined. In this paper we will determine the circumstances in which the optional splitting formula is valid. We will then develop practical sufficient conditions for that validity. Incidentally, our results reveal a close relationship between the optional splitting formula and several measurability questions encountered in credit risk modeling. That relationship allows us to provide simple answers to these questions.