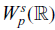1 results
Well-posedness of the Muskat problem in subcritical Lp-Sobolev spaces
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 18 January 2021, pp. 224-266
-
- Article
- Export citation
-
We study the Muskat problem describing the vertical motion of two immiscible fluids in a two-dimensional homogeneous porous medium in an Lp-setting with p ∈ (1, ∞). The Sobolev space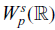
$W_p^s(\mathbb R)$
with s = 1+1/p is a critical space for this problem. We prove, for each s ∈ (1+1/p, 2) that the Rayleigh–Taylor condition identifies an open subset of
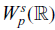$W_p^s(\mathbb R)$
within which the Muskat problem is of parabolic type. This enables us to establish the local well-posedness of the problem in all these subcritical spaces together with a parabolic smoothing property.
