1 results
Lacunary Interpolation by Fractal Splines with Variable Scaling Parameters
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 20 February 2017, pp. 65-83
- Print publication:
- February 2017
-
- Article
- Export citation
-
For a prescribed set of lacunary data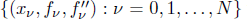
with equally spaced knot sequence in the unit interval, we show the existence of a family of fractal splines 
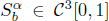satisfying 
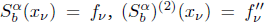for v = 0, 1, … ,N and suitable boundary conditions. To this end, the unique quintic spline introduced by A. Meir and A. Sharma [SIAM J. Numer. Anal. 10(3) 1973, pp. 433-442] is generalized by using fractal functions with variable scaling parameters. The presence of scaling parameters that add extra “degrees of freedom”, self-referentiality of the interpolant, and “fractality” of the third derivative of the interpolant are additional features in the fractal version, which may be advantageous in applications. If the lacunary data is generated from a function Φ satisfying certain smoothness condition, then for suitable choices of scaling factors, the corresponding fractal spline 
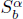satisfies 
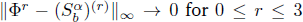, as the number of partition points increases.
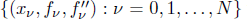with equally spaced knot sequence in the unit interval, we show the existence of a family of fractal splines 
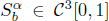satisfying 
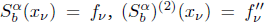for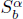 
satisfies 
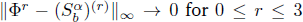, as the number of partition points increases.