1 results
Recurrence criteria for multi-dimensional Markov chains and multi-dimensional linear birth and death processes
-
- Journal:
- Advances in Applied Probability / Volume 8 / Issue 1 / March 1976
- Published online by Cambridge University Press:
- 01 July 2016, pp. 58-87
- Print publication:
- March 1976
-
- Article
- Export citation
-
Criteria are established for a discrete-time Markov process {Xn}n≧0 in Rd to have strictly positive, respectively zero, probability of escaping to infinity. These criteria are mainly in terms of the mean displacement vectors μ(y) = E{Xn+1|Xn = y} – y, and are essentially such that they force a deterministic process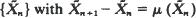
w.p.1 to move off to infinity, respectively to return to a compact set infinitely often. As an application we determine of most two-dimensional birth and death processes with rates linearly dependent on the population, whether they can escape to infinity or not.
w.p.1 to move off to infinity, respectively to return to a compact set infinitely often. As an application we determine of most two-dimensional birth and death processes with rates linearly dependent on the population, whether they can escape to infinity or not.