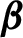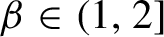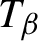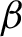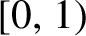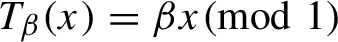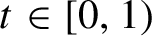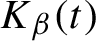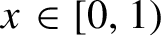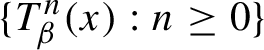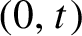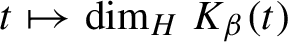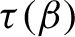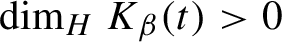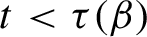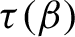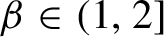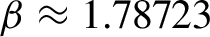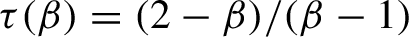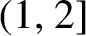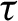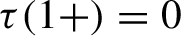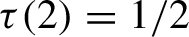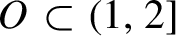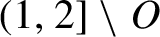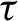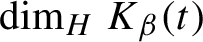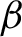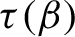Given 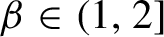\beta \in (1,2]$\beta \in (1,2]$ , let 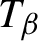T_{\beta }$T_{\beta }$ be the 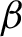\beta $\beta$ -transformation on the unit circle 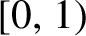[0,1)$[0,1)$ such that 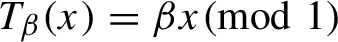T_{\beta }(x)=\beta x\pmod 1$T_{\beta }(x)=\beta x\pmod 1$ . For each 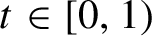t\in [0,1)$t\in [0,1)$ , let 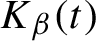K_{\beta }(t)$K_{\beta }(t)$ be the survivor set consisting of all 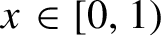x\in [0,1)$x\in [0,1)$ whose orbit 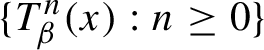\{T^{n}_{\beta }(x): n\ge 0\}$\{T^{n}_{\beta }(x): n\ge 0\}$ never hits the open interval 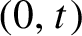(0,t)$(0,t)$ . Kalle et al [Ergod. Th. & Dynam. Sys. 40(9) (2020) 2482–2514] proved that the Hausdorff dimension function 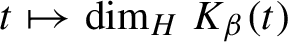t\mapsto \dim _{H} K_{\beta }(t)$t\mapsto \dim _{H} K_{\beta }(t)$ is a non-increasing Devil’s staircase. So there exists a critical value 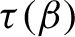\tau (\beta )$\tau (\beta )$ such that 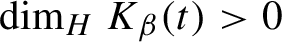\dim _{H} K_{\beta }(t)>0$\dim _{H} K_{\beta }(t)>0$ if and only if 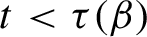t<\tau (\beta )$t<\tau (\beta )$ . In this paper, we determine the critical value 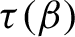\tau (\beta )$\tau (\beta )$ for all 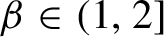\beta \in (1,2]$\beta \in (1,2]$ , answering a question of Kalle et al (2020). For example, we find that for the Komornik–Loreti constant 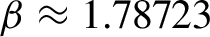\beta \approx 1.78723$\beta \approx 1.78723$ , we have 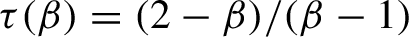\tau (\beta )=(2-\beta )/(\beta -1)$\tau (\beta )=(2-\beta )/(\beta -1)$ . Furthermore, we show that (i) the function \tau : \beta \mapsto \tau (\beta )$\tau : \beta \mapsto \tau (\beta )$ is left continuous on 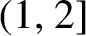(1,2]$(1,2]$ with right-hand limits everywhere, but has countably infinitely many discontinuities; (ii) 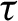\tau $\tau$ has no downward jumps, with 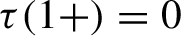\tau (1+)=0$\tau (1+)=0$ and 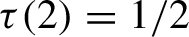\tau (2)=1/2$\tau (2)=1/2$ ; and (iii) there exists an open set 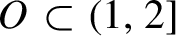O\subset (1,2]$O\subset (1,2]$ , whose complement 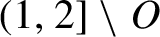(1,2]\setminus O$(1,2]\setminus O$ has zero Hausdorff dimension, such that 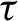\tau $\tau$ is real-analytic, convex, and strictly decreasing on each connected component of O. Consequently, the dimension 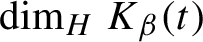\dim _{H} K_{\beta }(t)$\dim _{H} K_{\beta }(t)$ is not jointly continuous in 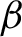\beta $\beta$ and t. Our strategy to find the critical value 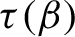\tau (\beta )$\tau (\beta )$ depends on certain substitutions of Farey words and a renormalization scheme from dynamical systems.