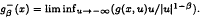1 results
On the solvability of semilinear differential equations at resonance
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 43 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 20 January 2009, pp. 103-112
-
- Article
-
- You have access
- Export citation

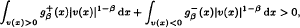
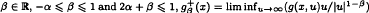 and
and