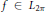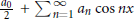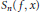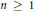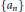Let $f\in \,{{L}_{2\pi }}$ be a real-valued even function with its Fourier series $\frac{{{a}_{0}}}{2}\,+\,\sum _{n=1}^{\infty }\,{{a}_{n}}\,\cos \,nx$, and let ${{S}_{n}}\left( f,x \right)$, $n\,\,\ge \,\,1$, be the $n$-th partial sum of the Fourier series. It is well known that if the nonnegative sequence $\{{{a}_{n}}\}$ is decreasing and 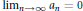${{\lim }_{n\to \infty }}\,{{a}_{n}}\,=\,0$, then

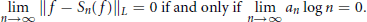$$\underset{n\to \infty }{\mathop{\lim }}\,{{\left\| f-{{S}_{n}}\left( f \right) \right\|}_{L}}=0\text{ifanyonlyif}\underset{n\to \infty }{\mathop{\lim }}\,{{a}_{n}}\log n=0.$$

We weaken the monotone condition in this classical result to the so-called mean value bounded variation (MVBV) condition. The generalization of the above classical result in real-valued function space is presented as a special case of the main result in this paper, which gives the 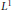${{L}^{1}}$-convergence of a function 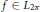$f\in {{L}_{2\pi }}$ in complex space. We also give results on 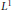${{L}^{1}}$-approximation of a function 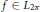$f\in {{L}_{2\pi }}$ under the MVBV condition.

The asymptotic behaviour of a superadditive bisexual Galton–Watson branching process is studied. Sufficient conditions for the almost sure and L1 convergence of the suitably normed process are given. Finally, a first approach to the study of the L1 convergence for a superadditive bisexual Galton–Watson branching process under the Z log+Z condition is considered.